9017. Бинарный
поиск – 1
Задан отсортированный
массив из n целых чисел.
Вам следует ответить на q запросов: сколько
раз заданное число x содержится
в массиве.
Вход. Первая
строка содержит два числа n и q (n,
q ≤ 106). Вторая
строка содержит n целых чисел,
отсортированных по возрастанию. Каждая из следующих q строк содержит одно значение x.
Все числа в массиве по модулю не превышают 109.
Выход. Для каждого значения x выведите в отдельной строке количество
его вхождений в массив.
|
Пример
входа 1 |
Пример
выхода 1 |
|
6 3 2 4 4 8 11 14 10 4 2 |
0 2 1 |
|
|
|
|
Пример
входа 2 |
Пример
выхода 2 |
|
8 4 -8 -8 -1 1 3 4 6 8 4 10 -4 -8 |
1 0 0 2 |
РЕШЕНИЕ
бинарный
поиск
Анализ алгоритма
Количество вхождений числа x в
отсортированный массив равно upper_bound(m,
m + n, x) – lower_bound(m, m + n, x).
Эти функции можно взять из библиотеки шаблонов STL или реализовать самостоятельно (например,
для Java).
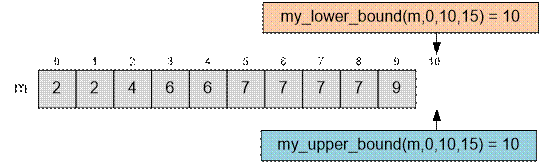
Пусть все n
элементов массива m находятся в ячейках от 0 до n – 1. В этом случае функции lower_bound и upper_bound могут возвращать
значения от 0 до n. Поэтому бинарный поиск следует выполнять в
этих пределах.
Реализация алгоритма
Объявим рабочий массив.
#define MAX 1000000
int m[MAX];
Читаем входные данные.
scanf("%d %d", &n,
&q);
for (i = 0; i < n; i++)
scanf("%d",
&m[i]);
Последовательно обрабатываем q запросов. Для каждого
запроса читаем значение x и выводим
количество его вхождений в массив m.
for (i = 0; i < q; i++)
{
scanf("%d",
&x);
res =
upper_bound(m, m + n, x) - lower_bound(m, m + n, x);
printf("%d\n",
res);
}
Реализация алгоритма –
собственные функции lower_bound,
upper_bound
#include <cstdio>
#include <algorithm>
#include <stdio.h>
#define MAX 1000000
int i, n, q, x, res;
int m[MAX];
int my_lower_bound(int *m, int start, int end, int x)
{
while (start < end)
{
int mid = (start + end) / 2;
if (x <= m[mid])
end = mid;
else
start = mid + 1;
}
return start;
}
int my_upper_bound(int *m, int start, int end, int x)
{
while (start < end)
{
int mid = (start + end) / 2;
if (x >= m[mid])
start = mid + 1;
else
end = mid;
}
return start;
}
int main(void)
{
scanf("%d %d", &n,
&q);
for (i = 0; i < n; i++)
scanf("%d", &m[i]);
for (i = 0; i < q; i++)
{
scanf("%d", &x);
res =
my_upper_bound(m, 0, n, x) – my_lower_bound(m, 0, n, x);
printf("%d\n", res);
}
return 0;
}
Java реализация
import java.util.*;
import java.io.*;
public class Main
{
static int my_lower_bound(int m[], int start, int end, int x)
{
while (start < end)
{
int mid = (start + end) / 2;
if (x <= m[mid])
end = mid;
else
start = mid + 1;
}
return start;
}
static int my_upper_bound(int m[], int start, int end, int x)
{
while (start < end)
{
int mid = (start + end) / 2;
if (x >= m[mid])
start = mid + 1;
else
end = mid;
}
return start;
}
public static void main(String[] args)
{
FastScanner con =
new FastScanner(new
InputStreamReader(System.in));
int n = con.nextInt();
int q = con.nextInt();
int m[] = new int[n];
for(int i = 0; i < n; i++)
m[i] = con.nextInt();
for(int i = 0; i < q; i++)
{
int x = con.nextInt();
int res = my_upper_bound(m,0,n,x) - my_lower_bound(m,0,n,x);
System.out.println(res);
}
}
}
class FastScanner
{
private BufferedReader br;
private StringTokenizer st;
public
FastScanner(InputStreamReader reader)
{
br = new BufferedReader(reader);
}
public String next()
{
while (st == null || !st.hasMoreTokens())
{
try
{
st = new StringTokenizer(br.readLine());
} catch (Exception e)
{
e.printStackTrace();
}
}
return st.nextToken();
}
public int nextInt()
{
return Integer.parseInt(next());
}
public double nextDouble()
{
return Double.parseDouble(next());
}
public void close() throws Exception
{
br.close();
}
}
Python реализация
import bisect
Читаем входные данные.
n, q = map(int, input().split())
lst = list(map(int, input().split()))
Последовательно
обрабатываем q запросов. Для каждого запроса читаем значение x и выводим количество его вхождений в список
lst.
for _ in
range(q):
x = int(input())
res =
bisect.bisect_right(lst, x) - bisect.bisect_left(lst, x)
print(res)